BANDERSNATCH BUFFET

by Steve Steinbock

This week I have a small smörgåsbord of items to spread on the table. Think of it as our very own Mad Tea Party, and I’m your March Hare. March? It’s only September.

The words “buffet” and “smörgåsbord” are both etymologically linked to the idea of a table. The former comes from a French word for “bench,” while the latter is Swedish for “butter-goose-board,” and refers to any sandwich board. I’m not sure what goose-butter (or buttered goose, for that matter) has to do with all-you-can-eat restaurants, but if you’ve looked at the kind of people who frequent smörgåsbords, the image of buttered geese brings a pretty funny image to mind.

Speaking of March Hares and Mad Tea Parties, I’ve been reading It Didn’t Mean Anything: A Psychoanalytic Reading of American Detective Fiction by Alexander N. Howe. The book is loaded with fascinating insights and observations, as well as pages of dense material that I’m not sure I understand. The book also includes some material that is pretty off-topic. Why, for instance, does he spend half-a-dozen pages discussing Mary Shelley’s Frankenstein to illustrate identification and trauma? Shelley’s novel is a Gothic classic. But it’s neither American nor detective fiction. Yet Howe never once mentions Stevenson’s Strange Case of Dr Jekyll and Mr Hyde, which is certainly a mystery and a crime novel, and its author did live for a time in the States. Seems to me it’s a pretty good illustration of identification and trauma as well.

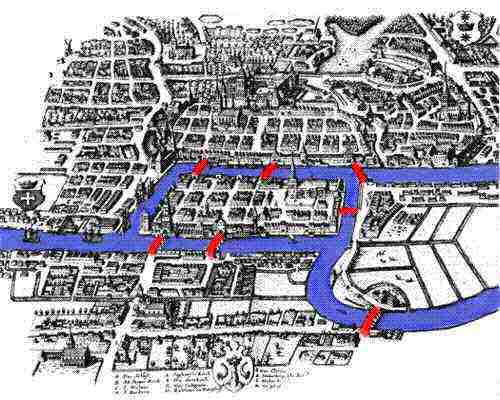
Early on in the book, Howe was using the word “topology” to describe the shape of fiction. I had to stop and look it up. Aha! It’s a branch of mathematics involving the study of objects in space, which is how I feel much of the time. Ruminating on a Möbius Strip is an example of topology. (which sounds like it could be a Somerset Maugham story, doesn’t it?) In 1736, the Swiss physicist Leonhard Paul Euler (who probably knew which side of his goose to butter) wrote a paper by this title that laid the groundwork for graph theory. The Prussian town of Königsberg was divided by a river in which two islands rested. Seven bridges connected the islands to the mainland and to each other. The challenge was to walk across all seven bridges without ever crossing the same bridge twice. Ultimately, the problem is impossible to solve without literally getting wet.

I learned so many things reading about topology. For instance, did you know that if you have a hairy sphere, it is impossible to brush the hair flat without there being a cowlick? But with a hairy bagel, it is possible to brush the hair completely flat. Try that one on your next smörgåsbord.

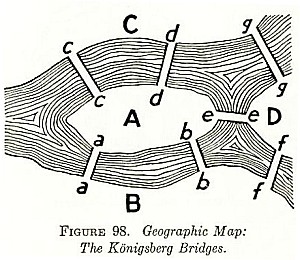Howe points out, quoting from Todorov’s “The Topology of Detective Fiction,” that classic detective stories contain two stories. The first is the crime, which in a classic detective story is never directly seen or told, and occurs either before the events of the story, or behind the curtains somewhere. The second story is that of the detective’s search for clues. As is the problem of the Seven Bridges of Königsberg. The second story, ultimately, is the only one that the reader gets to read. Think of the crime as cause and the clues as effects. Just like a diagnostician trying to determine a disease from the symptoms, the classical detective guides the reader on a path from effect to cause. I have no idea how one would draw a picture of this, but I’ll bet it’s as complicated as the Seven Bridges of Königsberg.

Finally, I came across a copy of the Great Detective Stories, published by Walter J. Black in 1928. This wonderful leatherbound gem looks like a Bible, with thin pages, and rounded, gilded edges. In its 842 pages it contains well over a hundred stories by the likes of Poe, Twain, Voltaire, Hugo, Pushkin, Dumas, Wilde, and others who aren’t typically counted among mystery writers. There’s no introduction or notes, and no editor is named. Just stories. Quite the smörgåsbord of stories, for that matter.

Now it is dinner time and I’m off to butter my goose.